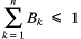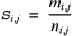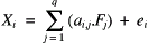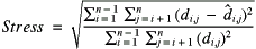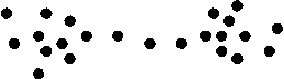This article uses embedded SP
fonts (SPIonic and SPDoric) for non-Roman text. Another version
which uses Unicode is located here.
Multivariate Statistical Analysis for Manuscript
Classification
J. C. Thorpe
Department of Computing and Mathematics
Manchester Metropolitan University
Manchester, UK
Abstract
The use of multivariate statistics for the analysis and
classification of New Testament manuscripts is examined, the problem
of coding the manuscripts for statistical analysis is considered, and
various coding schemes are presented. The operation and suitability of
a number of statistical techniques for manuscript classification is
also discussed.
Introduction
1. This article considers the statistical
techniques available for use in the classification of New Testament
manuscripts. The techniques described and evaluated are not novel, but
are used routinely by statisticians for a number of purposes. They
are implemented on computers in a wide variety of general purpose
statistical packages.
2. The process of classifying New
Testament manuscripts aims to identify groups and subgroups of
manuscripts with similar characteristics. Statistical analysis will
not guarantee a full genealogical classification of the available
manuscripts; at best it will show the degree to which manuscripts are
related and will highlight apparent clusters of manuscripts.
3. New Testament manuscripts contain many
variation units. In this paper, a variation unit is referred to as a
locus. Each locus has at least two possible readings; indeed, in some
cases there can be six or more different readings for the same
locus. Every manuscript has one reading at each locus. One of the
major problems of analysis is that for many manuscripts there are
lacunae. The full range of readings at many of the loci is therefore
not known.
Why Use Statistical Techniques?
4. Manuscripts are the product of
transcription by copyists, whose errors were the result of human
failings. It may thus seem odd to use mathematical techniques to
analyse the copyists' work; however, the sheer number of variations
makes it effectively impossible for the unaided human mind to carry a
full representation of the variations for even a single book. For this
reason, a formal method of tracking and investigating the variation
has obvious merits.
5. Statistical methods for investigating
manuscript relationships have the following advantages:
6. Objectivity: A statistical
technique will produce the same result no matter who carries it
out. It cannot be affected by the preconceptions of the person who
applies the technique, although a scholar could apply an inappropriate
technique or interpret the outcome of the technique incorrectly. The
results of statistical analysis are repeatable.
7. Rigour: The results of
statistical analysis are achieved through an open set of logical steps
which can be inspected by anyone who wishes to do so. Assumptions are
stated as part of the analysis and the effect of changing these
assumptions can be investigated.
8. Comprehensiveness:
Statistical techniques can, by using computers, handle very large
quantities of data; a large study can be carried out almost as easily
as a small one.
9. Scholars using non-statistical
methods strive to produce results with these characteristics. When
appropriate statistical techniques are used, these features are an
automatic result of the analysis.
10. There are, however, limits to the use
of statistical methods. They can only test hypotheses that have
already been formulated by human beings. Human imagination is required
to devise questions that can be expressed in rigorous terms and
investigated statistically. There can also be a problem with the
interpretation of the results of statistical analysis; the output of a
statistical procedure may need human interpretation to decide its
significance in terms of textual criticism.
Types of Data
11. Whether or not a statistical technique
is appropriate depends on the kind of data to be analysed. This
section introduces the kinds of data encountered in statistical
analysis.
12. Categorical data (also known as
nominal data): In data of this kind, the value assigned to a
variable has no meaning other than to indicate a particular fact
associated with the object. In particular, categorical data cannot be
used to provide a natural order for observations. For example,
consider the manuscripts A, B, and C. One variable which could be
associated with these manuscripts is current location (A is in London,
B is in the Vatican, and C is in Paris). One could code this data as 1
= London, 2 = Vatican, and 3 = Paris, but the values 1, 2, and 3 are
purely arbitrary. One cannot use the codes to order the data in any
meaningful way; that is, one cannot conclude that Paris is "more
than" London because its code has a higher value.
13. Ordinal data: Data of this
kind can be used to place observations in order, but the magnitude of
the data has no absolute meaning. For example, consider manuscripts A,
B, and E. B is the oldest, A is the second oldest, and E is the
youngest. One could code these facts by assigning the value 1 to the
oldest manuscript, 2 to the middle manuscript, and 3 to the most
recent. Sorting the manuscripts into numerical order based on this
variable would place them in age order, but no further information can
be gained from the code. There is a similarity between ordinal data
and nominal data in that neither can be used for arithmetic
calculation. (Some class both nominal and ordinal data as categorical
data, but most statisticians use the term categorical data to refer to
nominal data alone.)
14. Cardinal data: For data of
this kind, the magnitude is meaningful and one can derive useful
information by subtracting two values. For example, manuscript dates
are cardinal data and subtracting two dates produces a meaningful
result.
15. Absolute data: Some
cardinal measures are absolute. When a measure is absolute, the ratio
between two values is meaningful as well as the difference. For
example, consider manuscripts B (4th century) and 075 (10th
century). The date is not absolute; dividing the date of one
manuscript by the date of the other has no meaning, but one can
calculate that B is six centuries older than 075 by subtraction. Thus
the date is a cardinal measure. The age of B is about 16 centuries and
that of 075 about 10 centuries. This is an absolute measure, and one
can calculate that B is about 1.6 times older than 075. That is, the
age of a manuscript is an absolute measure.
Binary Measures
16. Categorical data with more than two
possible states is sometimes called multistate data. By contrast, a
binary measure can adopt only two values, typically zero or one. Any
discrete measure can be represented as a combination of binary
measures without loss of information. Nevertheless, care needs to be
taken when analysing data that has been recoded as binary
variables.
17. The most common use of binary
variables is as an alternative representation of categorical data.
When this is done, a categorical variable V with n states (v1,
v2, ... , vn) is coded as n binary variables
B1, B2, ... , Bn such that:
Bk = 1 if V = vk and
Bk = 0 if V ≠ vk.
18. In this representation, only one of
the binary variables B1, B2, ... , Bn
may have the value one at any given time. This requirement is
represented by the constraint:
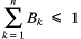
19. One of the problems with using a
binary representation of data is that each variable transformed into
a set of binary variables introduces another constraint into the
formal system representing the data.
Example
20. Using the code 1 = London,
2 = Vatican, and 3 = Paris, the current locations of manuscripts A, B,
and C can be denoted by the variable LOCk, where k ∈
{A, B, C}. The data can be recoded as the set of binary variables
LONk, VATk, and PARk with the added
constraint that LONk + VATk + PARk =
1:
| k |
LOCk |
LONk |
VATk |
PARk |
| A |
1 |
1 |
0 |
0 |
| B |
2 |
0 |
1 |
0 |
| C |
3 |
0 |
0 |
1 |
Objects and Variables
21. Multivariate statistics makes use of
the concepts of object and variable. Multivariate data
consists of observations made on a set of objects using a number of
variables--hence the term 'multivariate'. An object is an entity which
is to be described or classified in the analysis; in the statistical
analysis of manuscripts, the objects being analysed are usually the
manuscripts themselves. A variable is a measure that varies from
object to object. One might use the readings at a particular set of
loci as variables to describe a set of manuscripts.
Coding Manuscripts for Statistical Analysis
22. A collation lists manuscript texts in
a parallel fashion to facilitate comparison of their readings. The usual
procedure is to list readings that vary from a base text such as the
Textus Receptus or the United Bible Societies Greek New
Testament. A less common alternative is to print the texts in
parallel columns.
23. For the purposes of statistical
analysis, it is necessary to recode manuscript collation data into a
form that can be handled by a statistical package. Usually, this means
coding the readings as numerical values. The simplest method assigns a
single categorical variable to each locus in the text at which variant
readings occur. Each reading for the locus is then assigned an
arbitrary and unique numerical value. The reading of any given
manuscript at this locus is then represented by the corresponding
numerical value.
Example
24. The fourth word of John
1:4 in UBS4 is h(=n. There are
two other variants: some witnesses (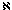 D
and others) have e)stin, while
Wsupp omits the word altogether. One could code the
variants as: 1 for h(=n, 2 for e)stin, and 3 for the omission. Using this coding
scheme, the respective values of the data variables for manuscripts D,
Wsupp, and B at this locus are 2, 3, and 1. Using
mathematical notation, one might define a data matrix
Dataj,k , where index j denotes the locus and index k
denotes the manuscript. If this locus is assigned the index 2, we
would write that Data2,D = 2,
Data2,Wsupp = 3, and Data2,B =
1.
D
and others) have e)stin, while
Wsupp omits the word altogether. One could code the
variants as: 1 for h(=n, 2 for e)stin, and 3 for the omission. Using this coding
scheme, the respective values of the data variables for manuscripts D,
Wsupp, and B at this locus are 2, 3, and 1. Using
mathematical notation, one might define a data matrix
Dataj,k , where index j denotes the locus and index k
denotes the manuscript. If this locus is assigned the index 2, we
would write that Data2,D = 2,
Data2,Wsupp = 3, and Data2,B =
1.
25. It can be difficult to decide what
constitutes a locus and what constitutes a variant reading. Taking the
start of the Lord's prayer at Luke 11:2 as an example, one might feel
that the words form a single sense unit and that this should be
counted as a single locus. However, another might decide that the
words form several logical units and that there should therefore be
several different loci, as in the UBS4 apparatus. Whether
variants are coded as one locus or several is one of the subjective
elements of statistical analysis.
26. A locus where more than one variant
exists could, of course, be coded as a family of binary variables with
an added constraint. It is important at this stage to include a
further binary variable to indicate whether the manuscript is extant
at this particular locus or whether there is a lacuna; where one of
the readings is a known omission from the text, a binary variable
should be set up to register the fact. The binary representation
should be the same whether it is coded directly from the text or is
generated from an earlier categorical representation.
27. A coded description of a manuscript
can be thought of as a multidimensional vector of values indicating a
single point in a vector space (manuscript space), with each
manuscript having a corresponding point in the space. However, there
are problems with this picture when each locus is described by a
single categorical variable and where some of the loci have more than
two readings. In such a situation, the value of the variable at the
locus does not represent the magnitude of a displacement in manuscript
space, which is the underlying assumption of the vector
representation. Unfortunately, many multivariate techniques assume
this model of data representation.
28. This problem can be alleviated to some
extent by coding loci with more than two variants as sets of binary
variables. However, even this is far from an ideal solution as each
locus thus represented implies a constraint. Coding an appreciable
portion of text can be expected to add many tens of such constraints
(or even hundreds), meaning that some areas of manuscript space are
infeasible; they cannot be occupied by a manuscript, even in
theory. As most multivariate techniques assume that data is continuous
and cardinal with no forbidden regions, the use of these techniques
must be considered suspect for both binary and multistate
representations.
Similarity and Dissimilarity matrices
29. One convenient and theoretically
acceptable method of expressing the degree of similarity between pairs
of manuscripts within a set of manuscripts being compared is the
similarity matrix S. An element si,j of this
matrix contains the number of loci where manuscript Zi has
the same reading as manuscript Zj, divided by the number of
loci where both texts are extant.
30. The similarity matrix S is
square, with one row and one column for each manuscript under
investigation. The diagonal elements si,i all have
the value one because they represent the similarity of a manuscript to
itself. Also, S is symmetric: si,j =
sj,i .
31. Some multivariate statistical
techniques can operate from a dissimilarity matrix D. This is
closely related to the similarity matrix S: every element
di,j of D has the value 1 -
si,j, where si,j is the
corresponding element of S.
32. It is relatively straightforward to
construct a similarity matrix from coded data in which each locus
corresponds to a single variable. Construction involves working
through all the loci under investigation, counting the number of loci
ni,j for which both manuscripts Zi and
Zj are extant, and the number of loci
mi,j for which both manuscripts have the same
reading. The similarity value si,j is given by the
ratio of the two values:
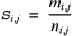
33. There can be problems in calculating a
correct value for ni,j when the manuscripts have
been coded using binary variables. The only way to be certain of
reaching a correct value is to include an additional binary variable
for each locus and each manuscript, indicating whether the text exists
there. If this variable is used, mi,j is the number
of variables where both manuscripts contain the value one and
ni,j is the number of loci at which both manuscripts
are marked as extant.
34. Note that the number of occasions when
two manuscripts both register a zero must not be counted in a
binary representation as this will increase the weighting given to
loci with more variants. Otherwise, the analysis will consider a locus
with, say, four variants to be twice as important as a locus with two,
and manuscripts may appear similar for no reason other than that they
have lacunae in the same places.
35. It is also important not to mix
representations. If a binary representation is used for some loci it,
must be used for all loci. Mixing representations confounds the
counting procedures used to generate a similarity matrix and produces
incorrect results.
Equivalence of Dissimilarity Matrices
36. Codex Sinaiticus is thought to change
character from "Western" to "Alexandrian" part way
through the Gospel of John1. Is this apparent change of textual
character real or can it be reasonably attributed to a random
fluctuation in affiliations? Another interesting question is whether a
supplement such as Wsupp has the same character as the
original MS. Such questions can be investigated by performing
statistical tests on dissimilarity matrices generated from manuscript
texts.
37. The Mantel test is used to investigate
whether two dissimilarity matrices are the same. It tests the
hypotheses:
H0: there is no relationship,
and
H1: there is a relationship between the two matrices.
38. Typical manuscript data do not fit
well with the underlying model of this test, where the null hypothesis
(i.e. H0) assumes no relation whatsoever between the
respective dissimilarity matrices. The question of relationship may be
better answered by applying repeated tests on the value of a
proportion using univariate statistics.
Principal Component Analysis
39. The purpose of principal component
analysis (PCA) is to describe a set of multivariate data in terms of a
set of uncorrelated variables, each of which is a linear combination
of the original variables. The new variables are called Principal
Components. These are listed in decreasing order of importance so
that the first principal component accounts for as much as possible of
the variation of the original data, the second principal component
accounts for as much as possible of the remaining variation, and so
on. The process continues until the number of principal components
generated equals the number of original variables in the data. The
hope is that the first few principal components will account for a
large proportion of the variation so that the objects can be well
described using a small number of variables.
40. Some regard PCA as an effective means
to investigate manuscript relationships. For example, Wieland
Willker2 performed PCA on the first chapters
John's Gospel. He indicates that plotting the first two principal
components reveals textual clusters which correspond to known text
types.
41. Nevertheless, there are problems
associated with using PCA to classify manuscripts:
- it assumes a space comprised of cardinal variables whereas
manuscript variants are represented by categorical variables. The
mismatch can be overcome to some extent by using a binary coding
scheme; however, this still leaves problems with forbidden regions,
loss of detail, and the introduction of random error.
- it has no simple means of coping with missing values. As many
manuscripts contain lacunae, PCA is not likely to produce a reasonable
description of more than a small proportion of manuscripts without a
strategy to handle missing values.
42. Willker avoids these pitfalls by only
using loci for which none of the manuscripts he is investigating have
lacunae. His work suggests that there is some value in using PCA to
investigate manuscript relationships. However, general use of the
technique is limited to places where no lacunae are present in the set
of MSS under investigation. In any event, there remain the problems of
non-cardinal data and implied constraints.
Factor Analysis
43. Like PCA, factor analysis attempts to
describe the full set of p variables X1, X2,
... , Xp in terms of a linear combination of other
variables. Unlike PCA--which retains the original number of variables
in its results--factor analysis is restricted to a smaller number q of
variables F1, F2, ... , Fq, this
number being specified by the analyst at the beginning. The new
variables are known as factors.
44. The model employed by factor analysis
is:
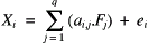
The coefficients ai,j are called the factor loadings
and ei is called the error term. It represents a
factor which is specific to the variable Xi. The data is
usually normalized so that each Xi has a mean of zero and
variance of one. Once normalization has been carried out, the error
terms also have a mean of zero.
45. Factor analysis attempts to choose
factors and factor loadings so that the factors are mutually
unrelated and the variation described by the error terms is
minimised. Very often the process will start with factors which are
the first q principal components and then gradually alter these to
minimise the contribution of the error terms; this process is called
"rotating the factors". The final factors are frequently,
but not always, close to the first few principal components.
46. Factor analysis requires all the
assumptions of PCA and therefore inherits all of its problems when
applied to manuscript data. Factor analysis does its best to represent
the data with the allocated number of dimensions. Because of this it
may provide a better fit than PCA where the map produced must have a
restricted number of variables.
Multidimensional Scaling
47. Multidimensional scaling treats the
dissimilarity matrix as a distance matrix which describes the
geography of a space containing the objects under investigation. It
generates a set of object coordinates that conform to these
'distances' as closely as possible, thereby allowing the objects to be
plotted on a map.
48. There are two varieties of
multidimensional scaling. The first, called classical scaling,
generates the coordinates using an algebraic procedure that assumes
that the 'distances' are Euclidean, although it is robust against
departures from this assumption3. The coordinates have the same
number of dimensions as the original data. As with PCA, the first few
dimensions are the most significant. Indeed, the results of PCA and
classical scaling are equivalent under certain circumstances4. Classical
scaling has already been used to investigate relationships among New
Testament manuscripts5.
49. The second variety, called non-metric
multidimensional scaling or ordinal scaling, seeks to find object
coordinates that conform to the rank order of the 'distances' rather
than their Euclidean values. This technique is therefore preferable in
situations where the Euclidean assumption is suspect. The number of
dimensions for the coordinates can be specified in advance. Two- or
three-dimensional representations are popular because the resulting
coordinates can be readily plotted on conventional maps.
50. The process attempts to minimize the
following stress measure:
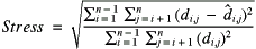
where n is the number of objects in the investigation
di,j is the distance between objects i
and j recorded in the dissimilarity matrix, and
d̂i,j is the distance between objects
i and j calculated from the generated coordinates.
51. The resulting map is considered to be
a good representation of the data if the stress value is less than 5%,
but a solution for which the value is less than 10% might be
considered acceptable in some circumstances. It is, however, unwise to
depend entirely on this measure6. A plot of the stress versus the
number of dimensions in the map can help to show the number of
variables required to provide an adequate description of the data.
52. A successful multidimensional scaling
exercise will generate coordinates which place similar manuscripts
close together and dissimilar manuscripts further apart. Plotting
these coordinates for a set of manuscripts will help to reveal any
groups that might exist. There is no reason why multidimensional
scaling should not be successfully applied to manuscript
classification as it requires nothing more than a dissimilarity matrix
to procede.
Cluster Analysis
53. The purpose of cluster analysis is to
classify objects into a relatively small number of clusters, the
intention being that members of the same cluster should be more
similar to one another than they are to objects outside the cluster. A
variety of approaches is available, some of which classify the objects
into a pre-determined number of clusters and others of which produce a
complete hierarchical family of relationships between objects.
54. A dendrogram is the usual
representation of the classification produced by a hierarchical
clustering technique. It is a tree diagram indicating the distances
between the clusters and sub-clusters involved.
55. The dendrogram produced by a
hierarchical clustering technique is not the same as a traditional
genealogy of manuscripts. The most obvious difference is that all the
manuscripts are at the tips of the tree--none of them is marked as an
ancestor of any of the others. Another point is that the branches in
the tree are always binary--there is never an ancestral node with
three or more descendants. One cannot take the dendrogram to be a tree
showing the chronological descent of the manuscripts concerned,
although it may be a useful tool in revealing such descent.
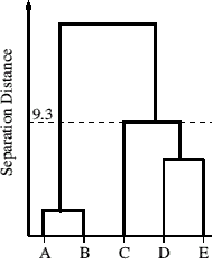
Fig. 1: Dendrogram
56. The objects are arranged along the
horizontal axis in a convenient order. In this example the letters are
purely arbitrary and do not correspond to actual manuscripts. The
vertical axis shows the distance between clusters that are linked at a
particular level. Here, the distance between the sub-cluster {D, E} and
the sub-cluster {C} is 9.3 units.
57. The dendrogram is useful for
identifying types, families, and clusters of manuscripts. There is
always a single top-level grouping which contains all manuscripts.
This all-encompassing group divides into smaller groups that may
themselves subdivide at lower levels in the diagram.
58. Agglomerative techniques are the
simplest and most often used form of hierarchical cluster analysis.
All such techniques employ the same basic process. At the beginning,
every cluster contains exactly one object. At each iteration, two
clusters are merged to form a larger cluster. The two chosen for
merging have the least value of an appropriate criterion for
expressing separation between clusters. The dendrogram records the
levels at which respective clusters merge, and the process repeats
until all of the objects are grouped together in a single cluster.
59. A range of criteria may be used to
measure cluster separation. Some require each object's spatial
coordinates while others can be calculated directly from the
dissimilarity matrix. The four most common techniques used for
agglomerative hierarchical clustering are:
- Nearest Neighbour or Single Linkage Clustering: The
distance between two clusters is the distance between the two closest
members of the respective clusters.
- Furthest Neighbour or Complete Linkage Clustering:
The distance between clusters is that between the two furthest members
of the respective clusters.
- Mean Distance or Group-Average Clustering: The
inter-cluster distance is the average of all distances between members
of the respective clusters.
- Centroid: This method requires a full set of coordinates to
be present for all of the objects to be classified. It calculates the
centroid coordinates of each cluster, then the Euclidean distances
between each pair of centroids. The pair with the least distance is
merged before proceeding to the next iteration.
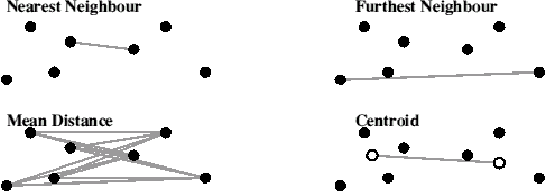
Fig. 2: Agglomerative Hierarchical Clustering
60. Centroid clustering requires
coordinates for every object. The other three methods can be performed
with nothing more than a dissimilarity matrix, making them useful
candidates for investigating manuscript relationships.
61. These methods do not necessarily
produce the same results. A study by Jardine and Sibson7 suggests
that nearest neighbour clustering has a strong theoretical foundation
whereas the other methods fall short; however, more recent studies
have questioned the validity of Jardine and Sibson's analysis. In
practice, mean distance is used more often than nearest neighbour
clustering.
62. Unfortunately, nearest neighbour
clustering suffers from a tendency to merge groups that are clearly
separate apart from a few intermediate objects. This effect is called
chaining, and results in a much less clear distinction between
clusters than one might otherwise expect. In extreme cases, dissimilar
clusters are linked together at a low level.
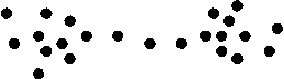
Fig. 3: Chaining
63. The furthest neighbour and
mean distance methods have been criticised because they tend to
favour clusters which are circular (or spherical) in the object space,
rather than elliptical clusters with high eccentricities. They also
have a tendency to form distinct clusters even when the objects
clearly belong to a single cluster. Nevertheless, they are resistant
to chaining.
Conclusion
64. This article surveys multivariate
techniques that may be applied to manuscript classification. These
techniques are not altogether novel, and have been used in a number of
manuscript studies. If used in an uncritical manner, they may produce
misleading or even spurious results. Care should be taken to avoid
techniques that assume a data model that is not appropriate for
manuscripts.
65. Of the techniques examined here,
multidimensional scaling and cluster analysis stand out as good
candidates for use in manuscript classification studies. They have the
potential to make very useful exploratory tools, provided that their
limitations are not overlooked.
Endnotes
1 Gordon D. Fee, "Codex
Sinaiticus in the Gospel of John", NTS 15/1 (1968):
23-44.
2 Wieland Willker,
"Principal Component Analysis of Manuscripts of the Gospel of
John", n.p. [cited 4 March 2002]. Online:
http://www-user.uni-bremen.de/~wie/pub/Analysis-PCA.html.
3 Christopher Chatfield and
Alexander J. Collins, Introduction to Multivariate Analysis
(London: Chapman and Hall, 1980), 190.
4 Chatfield and Collins,
Introduction, 201.
5 See, for example, Timothy
J. Finney, "The Ancient Witnesses of the Epistle to the
Hebrews" (Ph.D. diss., Murdoch University, 1999). Online:
http://purl.org/tfinney/thesis.
6 Chatfield and Collins,
Introduction, 207.
7 N. Jardine and R. Sibson,
Mathematical Taxonomy (New York: Wiley, 1971).
Bibliography
Chatfield, Christopher, and Alexander J. Collins. Introduction to
Multivariate Analysis. London: Chapman and Hall, 1980.
Everitt, B. S. Cluster Analysis. London: Edward Arnold, 1998.
Everitt, B. S., and G. Dunn. Applied Multivariate Data
Analysis. London: Edward Arnold, 2000.
Fee, Gordon D. "Codex Sinaiticus in the Gospel of John: A
Contribution to Methodology in Establishing Textual
Relationships". New Testament Studies 15/1 (1968):
23-44.
Finney, Timothy J. "The Ancient Witnesses of the Epistle to
the Hebrews: A Computer-Assisted Analysis of the Papyrus and Uncial
Manuscripts of pros ebraious". Ph.D. diss., Murdoch University,
1999. Online http://purl.org/tfinney/thesis.
Griffith, John G. "Numerical Taxonomy and Some Primary
Manuscripts of the Gospels". Journal of Theological Studies 20/2
(1969): 389-406.
_______ "Non-stemmatic Classification of Manuscripts by
Computer Methods". Colloques internationaux du CNRS 579--La
pratique des ordinateurs dans la critique des textes, 74-86.
Jardine, N., and R. Sibson. Mathematical Taxonomy. New York:
Wiley, 1971.
Kvalheim, O. M., D. Apollon, and R. H. Pierce. "A
Data-analytical Examination of the Claremont Profile Method for
Classifying and Evaluating Manuscript Evidence". Symbolae
Osloenses 63 (1988): 133-144.
Manly, B. F. J. Multivariate Statistical Methods. London:
Chapman and Hall, 1994.
Spencer, Matthew, and Christopher J. Howe. "Estimating Distances
between Manuscripts Based on Copying Errors". Literary and
Linguistic Computing 16/4 (2001): 467-484.
Willker, Wieland. "Principal Component Analysis of Manuscripts
of the Gospel of John". No pages [cited 4 March 2002]. Online:
http://www-user.uni-bremen.de/~wie/pub/Analysis-PCA.html.
© 2002 TC: A Journal of Biblical Textual Criticism
http://purl.org/TC/vol07/Thorpe2002.html
Last modified: Tue Jul 16 10:15:50 EDT 2002
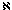 D
and others) have e)stin, while
Wsupp omits the word altogether. One could code the
variants as: 1 for h(=n, 2 for e)stin, and 3 for the omission. Using this coding
scheme, the respective values of the data variables for manuscripts D,
Wsupp, and B at this locus are 2, 3, and 1. Using
mathematical notation, one might define a data matrix
Dataj,k , where index j denotes the locus and index k
denotes the manuscript. If this locus is assigned the index 2, we
would write that Data2,D = 2,
Data2,Wsupp = 3, and Data2,B =
1.
D
and others) have e)stin, while
Wsupp omits the word altogether. One could code the
variants as: 1 for h(=n, 2 for e)stin, and 3 for the omission. Using this coding
scheme, the respective values of the data variables for manuscripts D,
Wsupp, and B at this locus are 2, 3, and 1. Using
mathematical notation, one might define a data matrix
Dataj,k , where index j denotes the locus and index k
denotes the manuscript. If this locus is assigned the index 2, we
would write that Data2,D = 2,
Data2,Wsupp = 3, and Data2,B =
1.